下面我将为你详细解释如何操作,并提供从简单到复杂的各种实例。
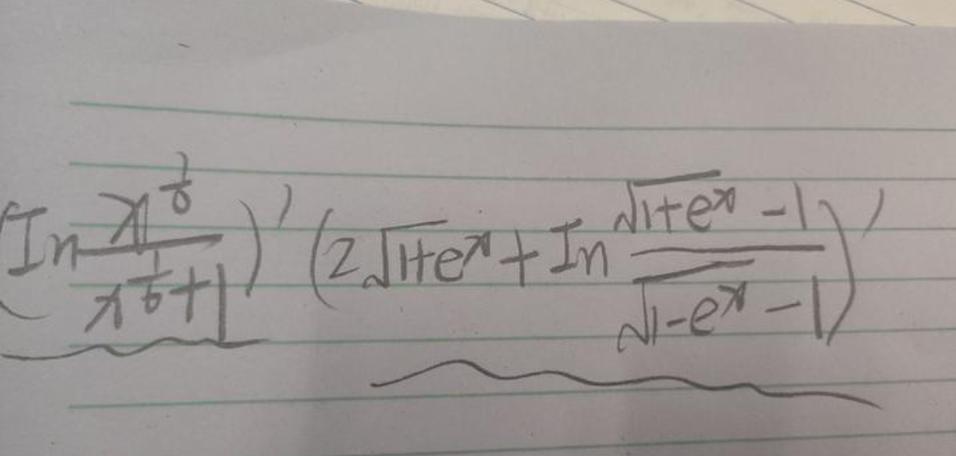
核心方法:使用关键词和语法
Wolfram Alpha 的核心是理解自然语言和数学语法,对于求参数范围,最直接的方法就是使用 这是最直接的形式,让你找到一个变量(参数)的取值范围。 语法: 示例 1:线性不等式
求 在 Wolfram Alpha 中输入: 或者 Wolfram Alpha 输出:
它会给出解集: 这是更常见的情况,方程中除了变量 语法: 示例 2:二次方程有实数根
求参数 逻辑分析: 有实数根意味着判别式 在 Wolfram Alpha 中输入:
你可以直接输入最终的不等式,也可以让 Wolfram Alpha 帮你完成判别式计算。 或者 Wolfram Alpha 输出:
求函数 逻辑分析: 求值域相当于求 在 Wolfram Alpha 中输入: Wolfram Alpha 输出:
它会计算判别式并解出 一个直角三角形的两条直角边的和为 10,求其面积的最大值。 逻辑分析: 在 Wolfram Alpha 中输入:
先求 得到 Wolfram Alpha 输出:
第一条命令给出 求实数 逻辑分析: 在 Wolfram Alpha 中输入: Wolfram Alpha 输出:
它会分别解出两个不等式,然后求交集。 通过掌握这些基本语法和思路,你就可以使用 Wolfram Alpha 轻松解决绝大多数关于参数范围的问题。solve 或 inequality
基本不等式求解
solve inequality [你的不等式] for [变量][变量]的范围 when [你的不等式]x 的范围,使得 3x - 5 > 10。

solve inequality 3x - 5 > 10 for xx 的范围 when 3x - 5 > 10x > 5,并用数轴图和区间表示法 (5, ∞) 直观地展示出来。
含参数的方程/不等式求解
x,还有一个未知参数 a,你需要根据条件,求出 a 的取值范围,使得方程有解、有唯一解、或者满足其他特定条件。
find [参数] such that [方程/不等式] has [条件]solve [方程/不等式] for [参数]a 的范围,使得方程 x² + 2ax + 4 = 0 有实数根。
D ≥ 0。
D = (2a)² - 4 * 1 * 4 = 4a² - 164a² - 16 ≥ 0solve x^2 + 2a*x + 4 = 0 has real solutions for asolve 4a^2 - 16 >= 0 for aa ≤ -2 或 a ≥ 2,用区间表示法表示为 (-∞, -2] ∪ [2, ∞)。
进阶应用与实例
实例 3:函数值域问题(转化为参数方程)
f(x) = (x² + 2x + 5) / (x² - 2x + 5) 的值域。
y 的范围,使得方程 y = (x² + 2x + 5) / (x² - 2x + 5) 有实数解 x,我们可以把 y 看作参数,然后解这个关于 x 的方程。find y such that y = (x^2 + 2x + 5) / (x^2 - 2x + 5) has real solutions for xy 的范围,得到 2/3 ≤ y ≤ 2。
实例 4:几何问题中的参数范围
a 和 b,则 a + b = 10。S = (1/2) * a * b。a 来表示 b (b = 10 - a),然后代入面积公式 S = (1/2) * a * (10 - a)。a 的二次函数,求其最大值,或者,我们可以求 a 的取值范围,因为边长必须为正数。a 的范围:solve a > 0 and 10 - a > 0 for a0 < a < 10。
然后求面积函数在此范围内的最大值:maximize (1/2) * a * (10 - a) for 0 < a < 100 < a < 10。
第二条命令给出最大值为 25,当 a = 5 时取得。
实例 5:复数问题
m 的范围,使得复数 z = (m² - 8m + 15) + (m² - 5m - 14)i 对应的点在复平面的第四象限。
m² - 8m + 15 > 0m² - 5m - 14 < 0solve m^2 - 8m + 15 > 0 and m^2 - 5m - 14 < 0 for m
m² - 8m + 15 > 0 的解是 m < 3 或 m > 5。m² - 5m - 14 < 0 的解是 -2 < m < 7。(-2, 3) ∪ (5, 7)。使用技巧与注意事项
solve, inequality, find, such that, for, when 等关键词可以帮助 Wolfram Alpha 更好地理解你的意图。for [变量] 指明你要求解的是哪个参数(变量)。总结表格
问题类型
Wolfram Alpha 输入示例
说明
基本不等式
solve 2x + 1 < 7 for x求解简单的一元一次不等式。
方程有实数根
find a such that x^2 + ax + 1 = 0 has real solutions利用判别式求解参数范围。
函数值域
find y such that y = x/(x^2+1) has real solutions for x将
y 视为参数,解关于 x 的方程。
几何问题
solve a > 0 and b > 0 and a + b = 10 for a结合实际问题,列出约束条件求解。
综合不等式
solve x^2 - 4 > 0 and x < 3 for x求多个不等式的交集(解集)。




